Elementos notables del triángulo

¡Hola a todos!

Hoy os traigo una entrada a modo de glosario, donde analizaremos los elementos notables de un triángulo. El triángulo puede definirse como la figura geométrica delimitada por tres líneas o como la forma que surge de la unión de tres puntos no alineados. Sean puntos o líneas los elementos de partida, lo que está claro es que como elementos básicos tendremos los siguientes:

Puntos                                                                     Líneas

                                        

·Puntos: los llamaremos vértices ya que delimitan la forma geométrica.

·Líneas: las llamaremos lados ya que delimitan la forma geométrica.

Tenemos que tener claro que la sumatoria de los ángulos interiores que forman los segmentos en cada vértice del triángulo será siempre de 180º.

Además, podemos clasificar los triángulos según sus lados:

Equilátero                                                     Isósceles                                                    Escaleno

                                            

·Equilátero: los tres lados son iguales.

·Isósceles: dos lados iguales.

·Escaleno: los tres lados son distintos.

O según sus ángulos:

Rectángulo                                                     Acutángulo                                                Obtusángulo

                                            

·Rectángulo: un ángulo recto, es decir, 90º

·Acutángulo: los tres ángulos son agudos, es decir, <90º

·Obtusángulo: uno de los ángulos es obtuso, es decir, >90º

Habiendo definidos ya el triángulo, sus elementos básicos y sus posibles clasificaciones, podemos ahora pasar a la definición de las rectas notables de un triángulo y la relación que éstas tienen con los puntos notables del mismo.

                      Rectas notables                                                            Puntos notables

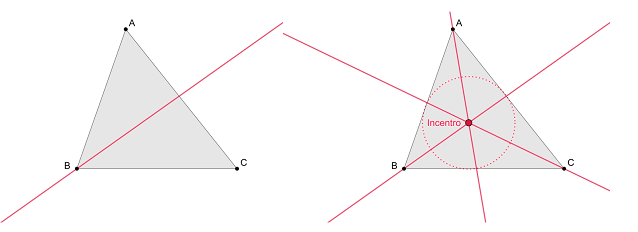Bisectriz                                                                                       Incentro

                                          

Bisectriz: es la recta que divide un ángulo en dos ángulos iguales. Desde la bisectriz de un ángulo definido por dos rectas se puede definir cualquier circunferencia que, con centro en la bisectriz, será tangente a las dos rectas. Es por tanto el lugar geométrico para estas circunferencias.

Incentro: se define como la intersección de las tres bisectrices de un triángulo. El incentro, independientemente del tipo de triángulo que sea, siempre queda definido en el interior del mismo. Podemos dibujar una circunferencia tangente a los tres lados (inscrita) cuyo centro es el incentro. Recuerda: Incentro - circunferencia inscrita

Mediana                                                                                       Baricentro

                                                        

Mediana: es el segmento que une el punto medio de un lado con el vértice opuesto. Por tanto, divide el triángulo en dos áreas iguales. Esto nos ayuda a entender la importancia del baricentro.

Baricentro: se define como la intersección de las tres medianas de un triángulo. El baricentro, independientemente del tipo de triángulo que sea, siempre queda definido en el interior del mismo. Se trata del centro de masas del triángulo, ya que cada una de las tres medianas divide el triángulo en dos masas idénticas. Como singularidad, el baricentro divide cada mediana en dos, de tal manera que la distancia del baricentro al vértice es siempre el doble que la del baricentro al punto medio.

Mediatriz                                                                                  Circuncentro

                                                        

Mediatriz: es la recta que, cruzándose al segmento de referencia en perpendicular, lo divide en dos segmentos iguales. Es por tanto el lugar geométrico para cualquier circunferencia que, con centro en la mediatriz, pasará por los dos puntos que definen el segmento.

Circuncentro: se define como la intersección de las tres mediatrices de un triángulo. En este caso, no se puede afirmar que su posición quede siempre en el interior del triángulo puesto que varía en función del tipo. Podemos dibujar una circunferencia que pase por los tres vértices (circunscrita) cuyo centro es el circuncentro. Recuerda: circuncentro - circunferencia circunscrita.

 Altura                                                                                         Ortocentro

                                                       

Altura: es el segmento que, desde el vértice opuesto, forma una perpendicular (ortogonal) con el segmento de referencia.

Ortocentro: se define como el punto de intersección de las tres alturas de un triángulo. En este caso, tampoco se puede afirmar que su posición quede siempre en el interior del triángulo puesto que varía en función del tipo. Recuerda: Ortocentro - rectas ortogonales.

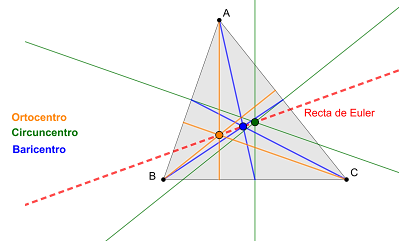
Para finalizar, cabe destacar que el ortocentro, baricentro y circuncentro de un triángulo quedan alineados cuando se superponen, definiendo lo que se denomina la Recta de Euler.

¡Nos leemos pronto!