Curvas cónicas.

Cuando hablamos de curvas cónicas, son 4 las diferentes figuras que podemos encontrarnos: circunferencia, elipse, parábola e hipérbola. Todas ellas responden a tres definiciones diferentes, por lo que tendremos que estar atentos a cuales son los datos de los que partimos. En este post ahondaremos sobre la elipse, pero generalizaremos posteriormente en cada apartado para comprender la similitud existente entre todas las curvas cónicas.

Así pues, estas son las definiciones que podemos encontrarnos:

· Trazado geométrico resultante de la intersección de un cono con un plano secante.

· Lugar geométrico de puntos de un plano cuya suma/resta de distancias a dos puntos fijos es siempre constante.

· Lugar geométrico de centros de circunferencias tangentes.

Por ello, resulta de especial relevancia tener estas figuras no sólo como curvas cónicas sino como lugar geométrico.

Veamos ahora cada una de las definiciones:

Trazado geométrico resultante de la intersección de un cono con un plano secante.

La figura resultante de la intersección de un cono (superficie cónica de revolución) y un plano secante depende de la relación existente entre dos ángulos.

α: Ángulo entre la generatriz del cono y el eje de revolución.

β: Ángulo entre una recta del plano secante y el eje de revolución.

        Circunferencia                        Elipse                            Hipérbola                        Parábola

α < β : Se forma una elipse, con la particularidad de que esa elipse será una circunferencia cuando β sea de 90º.

α = β : Se forma una parábola.

α < β : Se forma una hipérbola.

Del análisis profundo de estas figuras obtenemos los puntos fundamentales a la hora de definir una curva cónica. Ese análisis requiere del entendimiento del posicionamiento de dos esferas en el interior del cono, pero no entraremos en ello. De sus relaciones de tangencias con el plano secante obtenemos los siguientes puntos interesantes:

F1 y F2: Focos de la cónica

V1 y V2: Vértices de la cónica

d: Directriz de la cónica.

Una vez conocidos los focos podemos entender la siguiente definición de las curvas cónicas.

Lugar geométrico de puntos de un plano cuya suma/resta de distancias a dos puntos fijos es siempre constante.

Sea cualquier punto de la curva cónica, la relación entre las distancias que existen a los focos es siempre constante y además en el caso de la elipse e hipérbola, es de valor 2a. Este valor equivale al eje mayor de la curva cónica.

Hipérbola

Elipse

Elipse: la suma de distancias desde un punto a cada foco es siempre constante y de valor 2a.

Parábola: la distancia de un punto al foco es la misma distancia que existe a la directriz de la curva.

Hipérbola: la resta de distancias desde un punto a cada foco es siempre constante y de valor 2a.

Conocida ya la importancia de ese valor 2a podemos pasar a la siguiente definición.

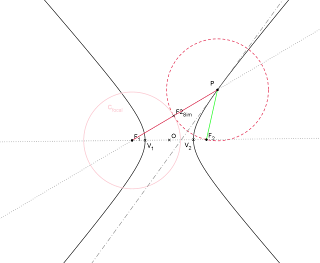
Lugar geométrico de centros de circunferencias tangentes.

¿Circunferencias tangentes a qué?  

A la circunferencia focal.

La circunferencia focal tiene por centro uno de los focos y por radio el valor 2ª. Así, elegido un punto P de la curva cónica, si trazamos segmentos a cada foco y luego los alineamos de tal forma que uno gire sobre el punto P hasta alinearse, la circunferencia formada por ese giro resulta tangente a la circunferencia focal.

Elipse como LG de centros de circunferencias tangentes.

Esto no solo sucede en la elipse, sino que también sucede en la hipérbola y la parábola. Sin embargo, en el caso de la parábola, puesto que uno de los focos está en el infinito la circunferencia focal con centro en ese foco y radio infinito se convierte en una recta, y es coincidente con la directriz de la curva.

Parábola como LG de centros
de circunferencias tangentes.

Hipérbola como LG de centros
de circunferencias tangentes.

Este punto de tangencia es también importante por la relación que guarda respecto del foco, y es que es el simétrico del mismo respecto de la bisectriz que forman los radios de la circunferencia con centro en P (radio PF2 Y radio PF2sim).

Tangente a una elipse

Tangente a una parábola

Tangente a una hipérbola

Esa bisectriz es, además, la tangente a la curva en el punto P.

Par concluir esta entrada ya solo nos queda introducir la circunferencia principal.

La circunferencia principal es aquella que con centro en O (centro de la cónica), pasa por los vértices de la cónica. Por tanto, tiene radio a.

Puesto que la principal tiene radio a y la focal 2a, si tomamos el foco que no es centro de la focal como centro de homotecia, podemos afirmar que ambas circunferencias son homotéticas, con una razón de homotecia 2 (o ½ depende como cada uno quiera mirarlo). En la figura se muestran algunos puntos interesantes a tener en cuenta.

Cfocal y Cprincipal, homotéticas con centro de homotecia F2

Si antes hablábamos de la importancia del punto simétrico del foco respecto de la bisectriz, ahora podemos entender que el punto medio entre ellos dos, que pertenece a la bisectriz, pertenece también a la circunferencia focal. Por ello, puede definirse ésta como circunferencia que contiene a los pies de las perpendiculares a la tangente trazadas desde el foco. Esto quiere decir que trazando una perpendicular a la tangente desde el foco se obtiene con la razón de homotecia al simétrico del foco.

Sucede de la misma forma en la parábola e hipérbola.

Con estos diagramas en mente, estamos preparados para resolver cualquier ejercicio de cónicas. 

¡Hasta la próxima!