Thales y Pitágoras, sentando las bases

¡Hola a todos!

En la entrada de hoy vamos a ver los aquellos teoremas que sentaron las bases de la geometría métrica: Thales y Pitágoras.

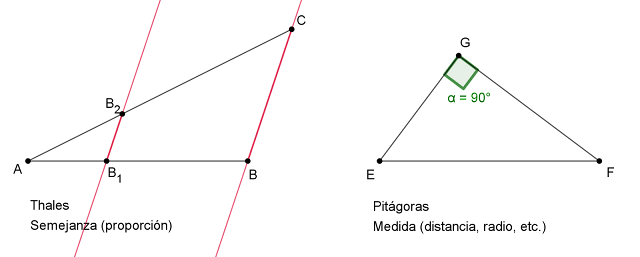
Al final de la entrada empezaremos ya a ver que todos los problemas que se nos presentan en la geometría métrica tienen su origen en uno de los dos. Deberemos saber identificar ante qué tipo de problema estamos, para determinar si es una semejanza (proporción) o una medida (distancia, radio, etc.) lo que se espera como respuesta. Siendo así, especificamos cómo asociamos los teoremas:

Thales

Dos figuras semejantes son aquellas que, siendo de diferente tamaño, conservan la misma razón entre sus partes.

Teorema de Thales: si en un triángulo se traza una línea paralela a cualquiera de sus lados,  el triángulo resultante es SEMEJANTE al triángulo dado.

Análogamente, si dos secantes (líneas rectas que intersecan en un punto) son intersecadas por líneas paralelas, los segmentos resultantes en cada secante son proporcionales.

Pitágoras

El teorema de Pitágoras se aplica únicamente en triángulos rectángulos y dice que, la suma de las áreas de los cuadrados resultantes de cada cateto, da como resultado el área del cuadrado cuyo lado es la hipotenusa.

Y por tanto, esta es la expresión matemática que corresponde a la expresión gráfica del teorema:

h²=a²+b² 

A continuación vamos a analizar la figura de un triángulo rectángulo entrelazando Thales y Pitágoras. De ello obtendremos el significado de la media proporcional.

Para ello, partiremos de la figura dada y la dividiremos en dos por el segmento altura respecto a la base, siendo la base el lado opuesto al ángulo recto o hipotenusa.

Los tres triángulos son semejantes, pero vamos a ver por qué, observando sus ángulos. Si en el triángulo base, denominamos β al ángulo en B y γ al ángulo en C, entonces el ángulo que se forma A para el segundo triángulo será γ y para el tercer triángulo β, puesto que los ángulos en B Y C no se alteran y el ángulo recto pasa a estar en la base del triángulo dado. Recordemos que la suma de los ángulos de un triángulo es siempre constante y es 180º. Veamos:

Debido a su semejanza, podemos establecer las siguientes relaciones proporcionales:

a/b=c/h=b/s

a/c=c/r=b/h

b/c=h/r=s/h

  
De las primeras dos igualdades podemos concluir que si a/b=b/s, entonces b²=a*s
                                                                             y que si a/c=c/r, entonces c²=a*r

 

Esto quiere decir que el cateto de un triángulo es la media proporcional de dos segmentos, que son: la hipotenusa y la proyección del propio cateto sobre la hipotenusa. 
A esto se le llama TEOREMA DEL CATETO.

 

De la misma forma, de la última igualdad obtenemos que si h/r=s/h, entonces h²=r*s.
Esto quiere decir que la altura de un triángulo rectángulo es la media proporcional de los segmentos en los que divide la hipotenusa. 
A esto se le llama TEOREMA DE LA ALTURA.

Ampliando el concepto de la media proporcional a la existencia de tres o cuatro segmentos obtenemos que:

z/e = f/z, entonces f=z²/e, lo que quiere decir que el segmento f es un TERCERO PROPORCIONAL  de los segmentos z y e.
z/e = f/z, entonces z² = e · f, lo que quiere decir que el segmento z es la MEDIA PROPORCIONAL  de los segmentos e y f.
z/e = f/g, entonces z = (e · f)/g, lo que quiere decir que el segmento z es un CUARTO PROPORCIONAL de los segmentos e, f y g.

Pero no nos quedamos únicamente aquí con la valía de Thales y Pitágoras para la geometría métrica. Vamos a definir, brevemente, el concepto de POTENCIA, que nos servirá para resolver posteriormente tangencias.

Potencia

Definimos la potencia como la “distancia” a una circunferencia desde un punto dado.

Difícil decir exactamente a qué punto de la circunferencia trazar esa distancia, ¿verdad? Concretemos: la potencia es el producto de dos distancias.

W² = dist_max*dist_min

Esta fórmula nos debería sonar ya de algo… pero vamos a seguir concretando. Conocemos el punto, conocemos el centro de la circunferencia, conocemos su radio. Entonces, si llamamos d al segmento que une punto y centro obtenemos lo siguiente:

W²= dist_max*dist_min=(d+R)*(d-R)=d²-R², es decir:

d²=W²+R²

Y es que, no deja de ser una medida eso que estamos buscando, por lo que Pitágoras tenía que andar detrás de todo esto. De esa expresión podemos deducir que el segmento d debe ser la hipotenusa de un triángulo rectángulo cuyos catetos serán W y R.

Gráficamente se vería tal que así:

El segmento de la potencia (W) es, por tanto, el segmento que une el punto dado con el punto de tangencia (T). No olvidemos que la potencia es un producto de distancias, por lo que será siempre W², siendo el segmento de potencia, por tanto, su raíz o lado Raíz(W²) = W.

Además, podemos afirmar que la potencia desde un punto es siempre constante. Es decir, que 

PA₁* PB₁= PA₂* PB₂= (PT)² o W²

Para demostrar esto gráficamente, debemos buscar semejanzas en esa imagen de arriba. Por tanto, estamos recurriendo nuevamente a Thales.

Hemos de saber que, partiendo de una recta secante a la circunferencia, cualquier ángulo que se forme entre los segmentos que unen cada punto que la secante interseca con la circunferencia y un punto cualquiera sobre la circunferencia, es el mismo.

Con esa aclaración hecha, podemos obtener que si la secante es el segmento A₁A₂, entonces el ángulo en B₁ y en B₂, es el mismo. Si además las dos rectas intersecan en el punto dado P, el ángulo que se forma entre ellas es el que es. Si sabemos que el ángulo en B₁ y en B₂ es el mismo y que el punto P es único y por ello el ángulo en él también, los triángulos que se forman con A₁ por un lado y con A₂ por otro deben ser iguales, ya que si comparten 2 ángulos, comparten los tres porque la suma ha de ser siempre 180º. Obtenemos entonces los siguientes triángulos:

De aquí, abstraemos lo siguiente: PA₁ / PA₂ = PB₂ / PB₁

Esto quiere decir que: PA₁* PB₁= PA₂* PB₂= (PT)² o W² y por tanto, se demuestra que la potencia desde un punto es siempre constante se trace la recta que se trace, siendo la más representativa aquella que define el punto de tangencia. 

Ya hemos sentado las bases para pasar en otra entrada al Problema Fundamental de Tangencia. Lo dejamos aquí por hoy.

¡Hasta la próxima!